Problema di Geometria

Dato un  triangolo ABC nel quale =2. Indicando con  e  le bisettrici degli angoli  e  rispettivamente e con   l’incentro del triangolo, posto   determinare il limite per x tendente a  del rapporto tra le aree dei triangoli e .

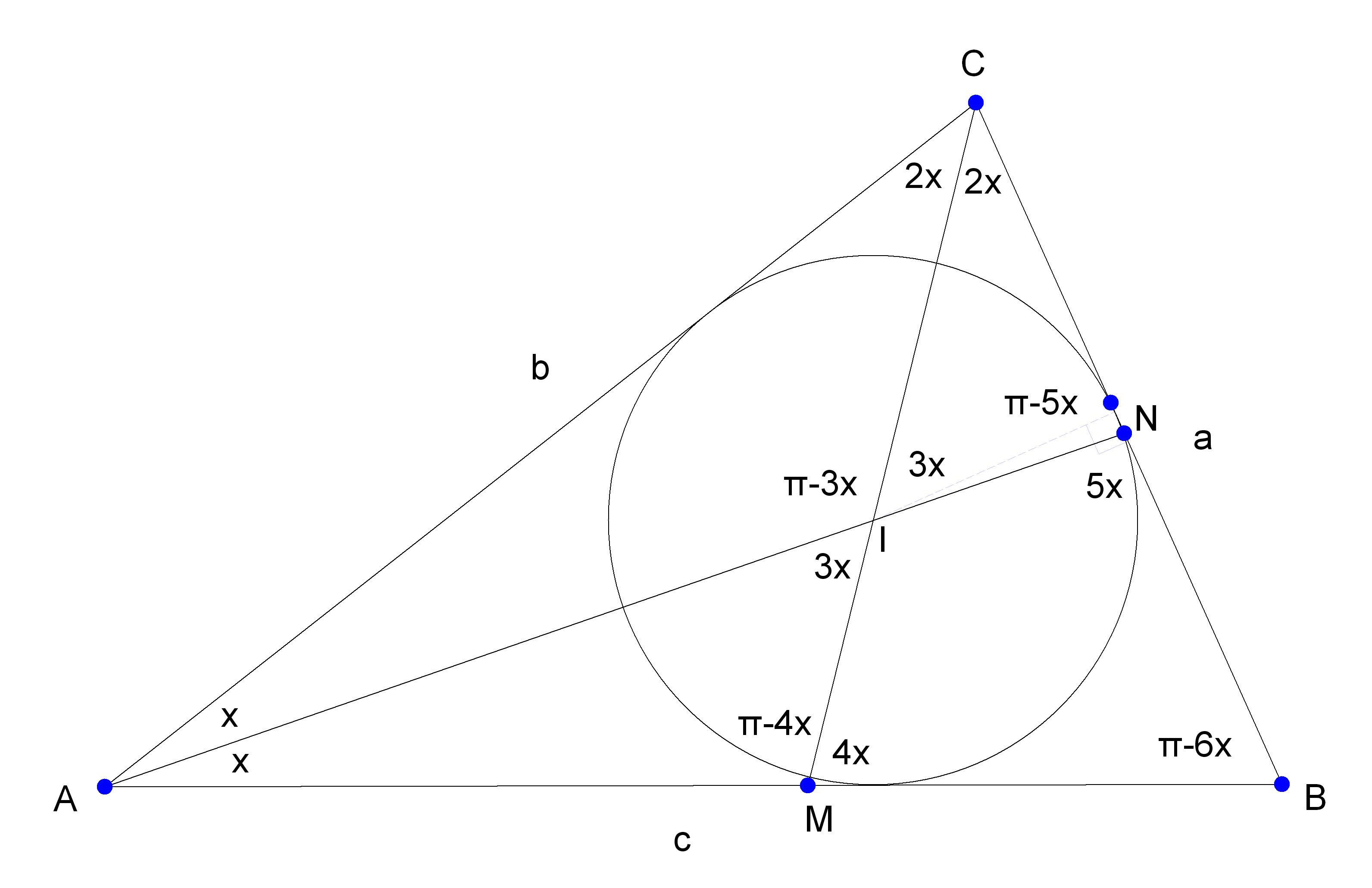
Poniamo  

Osservando che  e che  possiamo calcolare l’angolo  che essendo supplementare di   sarà pari a 3x. Pertanto . L’angolo  essendo opposto al vertice di  sarà anche esso pari a 3x. Osserviamo poi che  ed . Con un ragionamento analogo si deduce che , notiamo inoltre che il triangolo  è isoscele e pertanto

Esplicitiamo adesso le aree dei triangoli  e  indicando con r il raggio della circonferenza inscritta di centro I possiamo scrivere:

 

 

Quindi

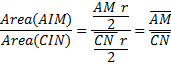
Applicando il teorema dei seni ai triangoli ACN e AMC possiamo scrivere:

Quindi

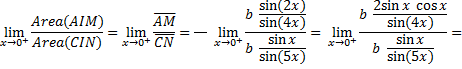
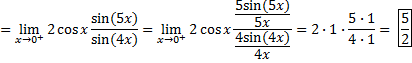
Avendo moltiplicato e diviso per x al fine di eliminare la forma indeterminata.